Binary search in C programming

In this article, you will learn the concept of binary search in C programming using arrays.

We have discussed two ways of searching an array.

• Linear Search
• Binary Search

The linear searching method works well with small and unsorted arrays. This process is slow and inefficient.

Thus, we are going to learn high-speed binary search technique.

Binary search in C programming using arrays

Binary search in C programming locates the middle element of the array and compares the search value.

If they are equal, it displays the subscript of that element, otherwise, the search is reduced to one-half.

If the search value is less than middle value of the array, the first half is searched, otherwise, the second half is searched.

This continues until the search value is equal to the middle value of the array or until the search value is not found.

How binary search in C programming works?

Let’s locate 18 in the following figure. It only takes 3 comparisons to find 18 which is much faster than other algorithms.

In a worst-case scenario, searching an array of 1023 elements takes only 10 comparisons using this method.

At first, it will divide 1024 by 2 giving 512 and then repeatedly dividing yields 256, 128, 64, 32, 16, 8, 4, 2 and 1.

[adsense1]

Please go through following  C programming articles to understand the concept of the program

• C programming if else
• C programming for loop
• C programming while
• C programming user-defined function

Binary search algorithm in C programming using arrays

#include <stdio.h>
#define SIZE 15

int binarySearch( int a[], int searchQuery, int low, int high);

int main()
{
   int data[ SIZE ]; //create array data
   int i; //variable for counter
   int query; //search value
   int temp;

   //generate data for array
   for (i = 0; i < SIZE; ++i)
      data[ i ] = 2 * i;

   printf("Enter number to search: ");
   scanf("%d", &query);

   //calling binary search user defined function
   temp = binarySearch(data, query, 0, SIZE - 1);

   //display result
   if ( temp != -1)
      printf("%d found in array element: %d", query, temp);
   else
      printf("%d not found.", query);

   return 0;
}

//user defined function for binary search
int binarySearch(int a[], int searchQuery, int low, int high)
{
   int middle; //variable for storing middle value

   //while loop continue until low subscript is greater then higher
   while( low <= high )
   {
      middle = ( low + high ) / 2; //determines middle element

      //if search query is same as middle element, return middle
      if ( searchQuery == a[middle])
         return middle;

      //if search is less than middle, set new high
      else if ( searchQuery < a[middle])
         high = middle - 1; //search lowest end of the array

      //if search query is greater than middle, set new low
      else
         low = middle + 1;
   }

   return -1; //search value not found
}

Output 1

Output 2

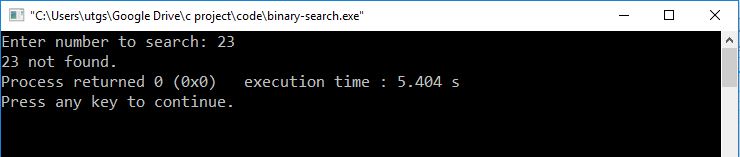
Explanation

In the above program, we have generated multiples of 2 up to 14 in an array data [].

There is a user-defined function binarySearch() for searching the array that takes four arguments.

In this program, only 3 comparisons are required to find the search value which is demonstrated above.